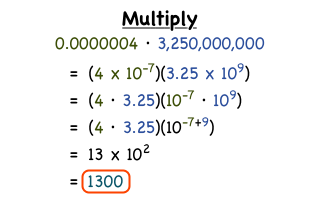Scientific Notation

Add Scientific Notation Calculator

Addition Scientific Notation

Instructions for use:

If the scientific notation is 45541 x 10⁶, you must use 45541e+6;
If the scientific notation is 0.44785 x 10^-10, you must use 0.44785e-10;
You will replace base 10 with the letter (e).

Scientific Notation 1:

Scientific Notation 2:

Scientific notation is related to the We can represent it as follows:

a . 10 ^b

a = coefficient / mantissa

10 = base

b = exponent / order of magnitude

It is possible to perform operations such as addition and subtraction with numbers represented in the form of scientific notation. Follow:

The addition in scientific notation

To add numerical terms written as scientific notation, the numbers must have the same order of magnitude, that is, the same exponent. When this happens, we can add the coefficients and conserve base ten power. See the general formula and some examples:

General formula for addition to scientific notation

(x . 10^a ) + (y . 10^a ) = (x + y) . 10^a

Example: Add the scientific notations below:
a) 1.2 x 10² + 11.5 x 10² = (1.2 + 11.5) x 10² = 12.7 x 10² = 1.27 x 10³
b) 0.23 x 10^-3 + 0.4 x 10^-3 = (0.23 + 0.4) x 10^-3 = 0.63 x 10^-3 = 6.3 x 10^-4
c) 200 + 3.5 x 10² = 2 x 10² + 3.5 x 10² = (2 + 3.5) x 10² = 5.5 x 10² → In this example, we had to convert 200 to 2. By doing this, we obtain the same order of magnitude for the two scientific notations.

https://www.youtube.com/watch?v=p0zVNTko7z4

About

This website was created to help students and curious people to solve problems with scientific notation. Addition, subtraction, division, multiplication and conversions.

Adding Scientific Notation Calculator