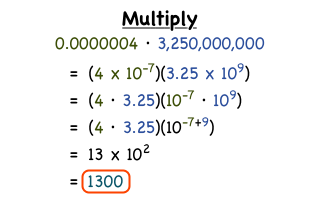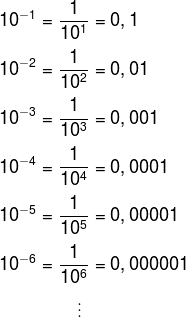Scientific Notation

Scientific Notation Converter

Decimal to Scientific Notation

Instructions for use:

If the decimal is 123445;
If the decimal is 1.43665;
If the decimal is 0.12001;
If the decimal is 2316.5567;
If the decimal is 0.00114011478;

Decimal Number:

https://www.youtube.com/watch?v=J-eQb7NMJFA

To transform a number into scientific notation, it is necessary to understand what are base powers 10. From the definition of power, we have to:

10⁰= 1

10¹= 10

10²= 10 · 10 = 100

10³= 10 · 10 · 10 = 1.000

10⁴= 10 · 10· 10· 10 = 10.000

10⁵= 10· 10· 10· 10· 10 = 100.000

Note that as the exponent increases, so does the number of zeros in the answer. Also see that the number in the exponent is the number of zeros that we have on the right. This is equivalent to saying that the number of decimal places moved to the right is equal to the power exponent. For example, 10¹⁰ is equal to 10,000,000,000.

Another case that we must analyze is when the exponent is a negative number.

Having reviewed the idea of base 10 power, we will now understand how to transform a number into scientific notation. It is important to emphasize that, regardless of the number, to write it in the form of scientific notation, we must always leave it with a significant figure.

Thus, to write a number in the form of scientific notation, the first step is to write it in the form of a product, so that a base 10 power (decimal form) appears. See the examples:

a) 0.0000034 = 3.4 x 0.000001 = 3.4 x 10^{– 6}

b) 134,000,000,000 = 134 x 1,000,000,000 = 134 x 10⁹

We agree that this process is not at all practical, so, in order to facilitate it, note that when we “walk” with the comma to the right, the base 10 exponent decreases the number of decimal places walked. Now, when we “walk” decimal places to the left, the base 10 exponent increases the number of walked places.

In summary, if the zeros are to the left of the number, the exponent is negative and coincides with the number of zeros; if the zeros appear to the right of the number, the exponent is positive and also coincides with the number of zeros.

Examples

a) The distance between the planet Earth and the Sun is 149,600,000 km.

Observe the number and see that, to write it in scientific notation, it is necessary to “walk” with the decimal point eight decimal places to the left, so the base 10 exponent will be positive:

149,600,000 = 1.49610⁸

b) The approximate age of planet Earth is 4,543,000,000 years.

Similarly, see that, to write the number in scientific notation, it is necessary to move 9 decimal places to the left, then:

4.543,000,000 = 4.54310⁹

c) The diameter of an atom is on the order of 1 nanometer, that is, 0.0000000001.

To write this number using scientific notation, we must move 10 decimal places to the right, so:

0,0000000001 = 1 x 10^-10

About

This website was created to help students and curious people to solve problems with scientific notation. Addition, subtraction, division, multiplication and conversions.